In our poker math and probability lesson it was stated that when it comes to poker; “the math is essential“. Although you don’t need to be a math genius to play poker, a solid understanding of probability will serve you well and knowing the odds is what it’s all about in poker. It has also been said that in poker, there are good bets and bad bets. The game just determines who can tell the difference. That statement relates to the importance of knowing and understanding the math of the game.
Practice defining ranges away from the table. Every player’s range is shaped by their previous.
- The river or river card is the final card dealt in a poker hand, to be followed by a final round of betting and, if necessary, a showdown. In Texas hold 'em and Omaha hold'em, the river is the fifth and last card to be dealt to the community card board, after the flop and turn.
- If you are facing an all-in or a river bet, you should follow three steps to decide whether to call or to fold: Step 1: Calculate the required equity. Required equity = price of calling / (pot size + price of calling) Step 2: Put your opponent on a range. Step 3: Calculate your equity against your opponent's range.
In this lesson, we’re going to focus on drawing odds in poker and how to calculate your chances of hitting a winning hand. We’ll start with some basic math before showing you how to correctly calculate your odds. Don’t worry about any complex math – we will show you how to crunch the numbers, but we’ll also provide some simple and easy shortcuts that you can commit to memory.
Basic Math – Odds and Percentages
Odds can be expressed both “for” and “against”. Let’s use a poker example to illustrate. The odds against hitting a flush when you hold four suited cards with one card to come is expressed as approximately 4-to-1. This is a ratio, not a fraction. It doesn’t mean “a quarter”. To figure the odds for this event simply add 4 and 1 together, which makes 5. So in this example you would expect to hit your flush 1 out of every 5 times. In percentage terms this would be expressed as 20% (100 / 5).
Here are some examples:
- 2-to-1 against = 1 out of every 3 times = 33.3%
- 3-to-1 against = 1 out of every 4 times = 25%
- 4-to-1 against = 1 out of every 5 times= 20%
- 5-to-1 against = 1 out of every 6 times = 16.6%
Converting odds into a percentage:
- 3-to-1 odds: 3 + 1 = 4. Then 100 / 4 = 25%
- 4-to-1 odds: 4 + 1 = 5. Then 100 / 5 = 20%
Converting a percentage into odds:
- 25%: 100 / 25 = 4. Then 4 – 1 = 3, giving 3-to-1 odds.
- 20%: 100 / 20 = 5. Then 5 – 1 = 4, giving 4-to-1 odds.
Another method of converting percentage into odds is to divide the percentage chance when you don’t hit by the percentage when you do hit. For example, with a 20% chance of hitting (such as in a flush draw) we would do the following; 80% / 20% = 4, thus 4-to-1. Here are some other examples:
- 25% chance = 75 / 25 = 3 (thus, 3-to-1 odds).
- 30% chance = 70 / 30 = 2.33 (thus, 2.33-to-1 odds).
Some people are more comfortable working with percentages rather than odds, and vice versa. What’s most important is that you fully understand how odds work, because now we’re going to apply this knowledge of odds to the game of poker.
The right kind of practice between sessions can make a HUGE difference at the tables. That’s why this workbook has a 5-star rating on Amazon and keeps getting reviews like this one: “I don’t consider myself great at math in general, but this work is helping things sink in and I already see things more clearly while playing.”
Instant Download · Answer Key Included · Lifetime Updates
Counting Your Outs
Before you can begin to calculate your poker odds you need to know your “outs”. An out is a card which will make your hand. For example, if you are on a flush draw with four hearts in your hand, then there will be nine hearts (outs) remaining in the deck to give you a flush. Remember there are thirteen cards in a suit, so this is easily worked out; 13 – 4 = 9.
Another example would be if you hold a hand like and hit two pair on the flop of . You might already have the best hand, but there’s room for improvement and you have four ways of making a full house. Any of the following cards will help improve your hand to a full house; .
The following table provides a short list of some common outs for post-flop play. I recommend you commit these outs to memory:
Table #1 – Outs to Improve Your Hand
The next table provides a list of even more types of draws and give examples, including the specific outs needed to make your hand. Take a moment to study these examples:
Table #2 – Examples of Drawing Hands (click to enlarge)
Counting outs is a fairly straightforward process. You simply count the number of unknown cards that will improve your hand, right? Wait… there are one or two things you need to consider:
Don’t Count Outs Twice
There are 15 outs when you have both a straight and flush draw. You might be wondering why it’s 15 outs and not 17 outs, since there are 8 outs to make a straight and 9 outs for a flush (and 8 + 9 = 17). The reason is simple… in our example from table #2 the and the will make a flush and also complete a straight. These outs cannot be counted twice, so our total outs for this type of draw is 15 and not 17.
Anti-Outs and Blockers
There are outs that will improve your hand but won’t help you win. For example, suppose you hold on a flop of . You’re drawing to a straight and any two or any seven will help you make it. However, the flop also contains two hearts, so if you hit the or the you will have a straight, but could be losing to a flush. So from 8 possible outs you really only have 6 good outs.
It’s generally better to err on the side of caution when assessing your possible outs. Don’t fall into the trap of assuming that all your outs will help you. Some won’t, and they should be discounted from the equation. There are good outs, no-so good outs, and anti-outs. Keep this in mind.
Calculating Your Poker Odds
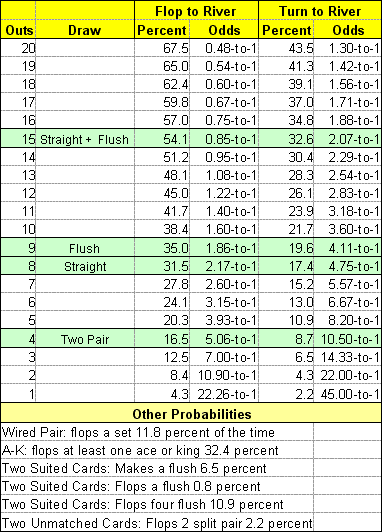
Once you know how many outs you’ve got (remember to only include “good outs”), it’s time to calculate your odds. There are many ways to figure the actual odds of hitting these outs, and we’ll explain three methods. This first one does not require math, just use the handy chart below:
Table #3 – Poker Odds Chart
As you can see in the above table, if you’re holding a flush draw after the flop (9 outs) you have a 19.1% chance of hitting it on the turn or expressed in odds, you’re 4.22-to-1 against. The odds are slightly better from the turn to the river, and much better when you have both cards still to come. Indeed, with both the turn and river you have a 35% chance of making your flush, or 1.86-to-1.
We have created a printable version of the poker drawing odds chart which will load as a PDF document (in a new window). You’ll need to have Adobe Acrobat on your computer to be able to view the PDF, but this is installed on most computers by default. We recommend you print the chart and use it as a source of reference. It should come in very handy.
Doing the Math – Crunching Numbers
There are a couple of ways to do the math. One is complete and totally accurate and the other, a short cut which is close enough.
Let’s again use a flush draw as an example. The odds against hitting your flush from the flop to the river is 1.86-to-1. How do we get to this number? Let’s take a look…
With 9 hearts remaining there would be 36 combinations of getting 2 hearts and making your flush with 5 hearts. This is calculated as follows:
(9 x 8 / 2 x 1) = (72 / 2) ≈ 36.
This is the probability of 2 running hearts when you only need 1 but this has to be figured. Of the 47 unknown remaining cards, 38 of them can combine with any of the 9 remaining hearts:
9 x 38 ≈ 342.
Now we know there are 342 combinations of any non heart/heart combination. So we then add the two combinations that can make you your flush:
36 + 342 ≈ 380.
The total number of turn and river combos is 1081 which is calculated as follows:
(47 x 46 / 2 x 1) = (2162 / 2) ≈ 1081.
Now you take the 380 possible ways to make it and divide by the 1081 total possible outcomes:
380 / 1081 = 35.18518%
This number can be rounded to .352 or just .35 in decimal terms. You divide .35 into its reciprocal of .65:
0.65 / 0.35 = 1.8571428
And voila, this is how we reach 1.86. If that made you dizzy, here is the short hand method because you do not need to know it to 7 decimal points.
The Rule of Four and Two
A much easier way of calculating poker odds is the 4 and 2 method, which states you multiply your outs by 4 when you have both the turn and river to come – and with one card to go (i.e. turn to river) you would multiply your outs by 2 instead of 4.
Imagine a player goes all-in and by calling you’re guaranteed to see both the turn and river cards. If you have nine outs then it’s just a case of 9 x 4 = 36. It doesn’t match the exact odds given in the chart, but it’s accurate enough.
What about with just one card to come? Well, it’s even easier. Using our flush example, nine outs would equal 18% (9 x 2). For a straight draw, simply count the outs and multiply by two, so that’s 16% (8 x 2) – which is almost 17%. Again, it’s close enough and easy to do – you really don’t have to be a math genius.
Do you know how to maximize value when your draw DOES hit? Like…when to slowplay, when to continue betting, and if you do bet or raise – what the perfect size is? These are all things you’ll learn in CORE, and you can dive into this monster course today for just $5 down…
Conclusion
In this lesson we’ve covered a lot of ground. We haven’t mentioned the topic of pot odds yet – which is when we calculate whether or not it’s correct to call a bet based on the odds. This lesson was step one of the process, and in our pot odds lesson we’ll give some examples of how the knowledge of poker odds is applied to making crucial decisions at the poker table.
As for calculating your odds…. have faith in the tables, they are accurate and the math is correct. Memorize some of the common draws, such as knowing that a flush draw is 4-to-1 against or 20%. The reason this is easier is that it requires less work when calculating the pot odds, which we’ll get to in the next lesson.
Related Lessons
By Tom 'TIME' Leonard
Tom has been writing about poker since 1994 and has played across the USA for over 40 years, playing every game in almost every card room in Atlantic City, California and Las Vegas.
Related Lessons
Related Lessons
Did you ever wonder what is all the maths that professional poker players seem to be doing in their head? Well a lot of the time they will be counting outs to see what chance they have of winning.
Learning the basics of counting outs is another step on your journey to becoming a proficient poker player. But first what exactly are poker outs?
An out is any card that will improve your hand to better than that of your opponent. A common example is when you have four hearts in your hand and need the fifth heart to complete the flush (i.e. a flush draw) . If you count the number of hearts left in the deck (13 total minus the 4 in your hand = 9), you know how many outs you have and can work out the probabaility of winning the hand.
So counting outs is just very basic addition and multiplication.
Another simple example is when you have a flush draw such as A♥ K♥ of hearts on T♥ 7♥ 2♠ – you currently only have Ace high but any heart will give you a flush.
There are 9 hearts in total which will complete your draw however one of those hearts (2♥) may give your opponent a full house.
You can also hit an ace (A♠, A♣, A♦) or king (K♠, K♣, K♦) but these cards aren’t always guaranteed to give you the best hand. Generally speaking, you only count the outs which are sure to give you the best hand.
Table Of Contents
- Considerations and additional points when counting outs
Counting Outs: The Process
The first question you need to ask yourself when counting outs is ’How many cards in the deck will give me the hand I want? ‘
For example if you have a flush draw you will have 9 outs, if you have a gut shot you will have 4 outs, and with an opened ended straight draw you have 8 outs. A table below summarizes each draw with number of outs.
| Draw type | Example hand | Example Board | No. of outs |
|---|---|---|---|
| Three of a kind draw | 5♥ 5 ♠ | A♦ 7♣ 2♥ | 2 |
| Gutshot straight draw | 7♥ 6♥ | A♣ 5♦ 3♠ | 4 |
| Open ended straight draw | K♠ Q♣ on | J♥ T♥ 2♣ | 8 |
| Flush draw | A♥ 2♥ | T♥ 7♣ 3♥ | 9 |
| Open ended & flush draw | J♥ T♥ | 9♥ 8♥3♠ | 15 |
Now that you know how many outs you have you need to actually use that number There is no point in calculating your outs if we aren’t going to use it in our decision making process.
The easiest way to do this is using the rule of 2 and 4…
The rule of 2 and 4
This rule is pretty simple.
To work out your equity or chance of winning when seeing the turn you multiply the number of outs by 2. Thus if we have 9 outs we will multiply that by 2 to get 18% equity.
For example if we are on the turn and want to know our chance of hitting by the river this is the method we would use.
To estimate your equity or chance of winning when on the flop you multiply the number of outs by 4. Again, if we have 9 outs we will multiply that by 4 to get 36% equity. For example if we are on the flop and want to know our chance of hitting by the river.
The rule of 2 and 4 is only an estimation for our equity but it is usually accurate giving our equity to within a percentage point or two.
Part of counting your outs is understanding if you are ahead or behind (and by how much) so it is important to understand your opponent's range. For more information on ranges see thefollowing link.
When we know our equity we can make a decision whether our hand is worth continuing with.
This method is actually pretty accurate, particularly for low numbers of outs. See the table below where I compared equity for each situation using the 2 and 4 method and equilab.
| Draw type | Equity on the flop | Equity on the turn | ||
|---|---|---|---|---|
| Rule of 2&4 | Equilab | Rule of 2&4 | Equilab | |
| Three of a kind draw | 8% | 9% | 4% | 5% |
| Gutshot straight draw | 16% | 18% | 8% | 10% |
| Open ended straight draw | 32% | 30% | 16% | 19% |
| Flush draw | 36% | 33% | 18% | 18% |
| Open ended & flush draw | 60% | 60% | 30% | 39% |
The above table assumes that only the the primary draw goes towards our chances of winning. In reality, you will have slightly more equity than the rule of 2 and 4 suggests as you will often have equity from backdoor draws and overcards.
The overall process for counting outs and calculating equity
- Determine what hand you have or could potentially have. If you are not sure of the hand rankings make sure you check them out
- Count how many cards will give you that hand
- Calculate your equity using the rule of 2 and 4
- Determine if your hand is worth continuing vs a bet by weighting your equity vs pot odds.
Considerations and additional points when counting outs
Double Counting
One must always be careful not to double count outs. With a big draw such as a straight and flush draw we will have 9 outs to the flush and 8 outs to the straight. However, of the straight draw outs there will be two which also complete the flush; thus we must remove these double counted outs.
As a result we no longer have 17 outs (9 flush + 8 straight), we now have 15 outs (9 flush + 6 straight or 7 flush + 8 straight)
The Double gutter
One interesting hand type is the double gutter. A double gutter is as the name suggests a double gut shot.
An example is when you have JT on AQ8 board. Any 9 or K will make you a straight. A double gutter can sometimes be difficult to spot, even for experienced players.
However, that makes them more powerful than other draws, as when you hit your hand it is more disguised. A more disguised hand is more likely to get paid off when you hit.
The Monster Draw
Another interesting hand type is the ‘monster’ draw. These are draws with typically 12 or more outs such as a flush draw + straight draw, or a flush draw plus pair type hand.
These hands have so many outs that it almost never wrong to commit all your chips (given you have a reasonable stack size).
The most powerful of all these hand types is the open ended straight flush draw- J♥T♥ on Q♥9♥5♣.
With this hand, not only do you have a flush and a straight draw but you have two cards which are the absolute nuts – you cannot ever be beaten if you hit the K♥ or the 8♥. The importance of these 2 outs cannot be underestimated.
One issue with monster draws is that the rule and two and four begins to break down- the rule overestimates the equity. Although there will be very few situations where you will be folding a big draw.
All Outs Are Not Equal – Anti-outs
Another aspect we need to take into account is that not all outs are created equal. Outs to the nuts (the strongest hand possible) are always the most sought after type of outs; unfortunately we won’t always have outs to the nuts.
In most cases we will count our flush draw out as a normal out but it can complete a full house for our opponent.
Take for example our opponent has 77 on T♥7♥2♠: we will count the 2♥ as an out when we have a heart flush draw.
However, it will improve our opponent's hand at the same time as ours; unfortunately for us that will be to a full house which beats a flush.
We will lose a lot of money in this example.
A further example of drawing to not nutted outs is the ‘dummy’ or bottom end of the straight. When we have the bottom two cards of a four to a straight, for example 87 on T95 flop, we will be dominated by a hand such as KQ; if a jack hits we will both complete a straight but KQ will have the nut straight, beating our lower straight.
As such, drawing to the upper end of the straight is much more powerful. Although, it is not always possible to avoid drawing to the dummy end of the straight. However, take into account they are less powerful than other straight draws and hence you should be less likely to proceed with them vs betting action.
Poker Equity On Turn And River Cruises
We can apply a similar thought process to overcard outs: AK on T52 board. If we hit our Ace or King on the turn we may not still have the best hand. Someone may have a set or two pair already or they might make two pair with the card which helps us.
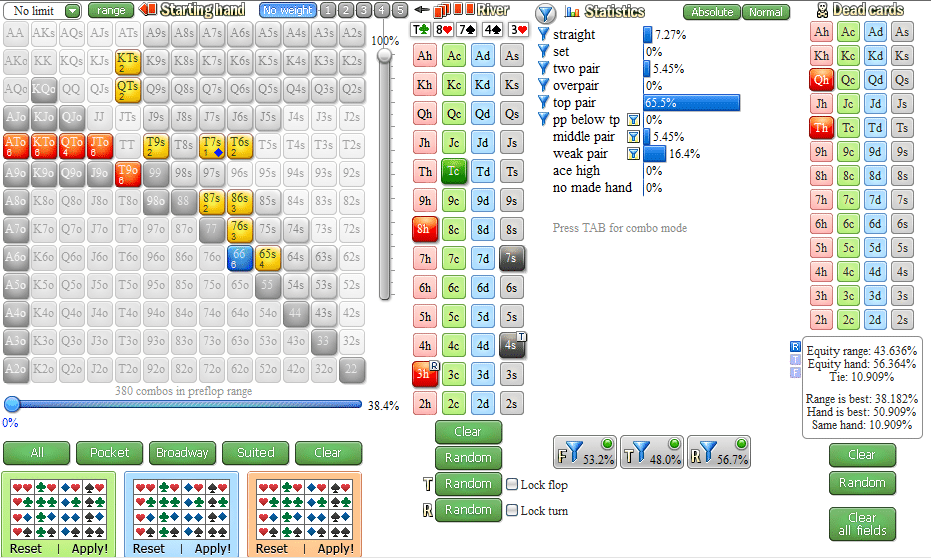
Counting Outs Real Life Example:
How many outs do we have here?
Our opponent has 44 and we have 9♥8♥ on T♥5♣3♥7♠ board.
- We have two overcards to our opponent so that is 3 outs for the 9 and 3 outs for the 8 for a total of 6.
- We have a J and a 6 to complete our straight which is 4 each for a total of 8.
- We also have a flush draw of which there is 13 hearts in total. We have 2 of them hearts, our opponent has one and there are two on the board. That leaves 8 hearts.
Poker Equity On Turn And River Flows
That gives a total of 22 outs..
Poker Equity On Turn And River Flow
However we have double counted some of the outs. The 6♥ and the J♥ are counted in the flush and the straight counts we made.
We should only count them once meaning that we now have a total of 20 outs. Using the rule of 2 and 4, we know that we have approximately 40% equity since we are on the turn.
That means we should be calling almost any sized bet on this turn if we knew our opponent had a pair of 4's on the board.
Pot Equity Poker
Conclusion
Counting outs is not the most difficult of tasks a poker player must perform; however but it is one of the most useful. If you know how to count and think about your outs you are well of some of the poker population.
Counting outs allows you to understand how likely you are to win the hand. This allow you to decide whether you want to continue versus a bet or raise and hence make more informed decisions at the poker table.
Poker Range Equity
The more likely to win the hand, the less likely you should be to fold.
Follow up this lesson with another on Pot Equity.